roofline model

定义 \[运算强度 = 运算量/访存量\] 运算量是 一个样本进行一次前向传播的浮点运算次数 访存量是 一个样本进行一次前向传播的内存交换数量

以运算强度为横轴、每秒浮点运算次数为纵轴画图，就能得到roofline

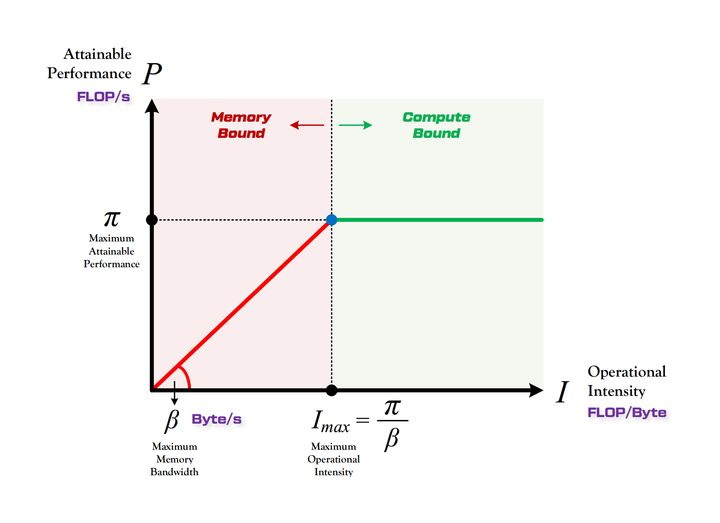算力决定屋顶的高度，带宽决定屋檐的斜率。

所有的计算对应的点都不会超过红绿线

红色部分叫做带宽瓶颈区域，模型计算强度达不到设备的最大性能是，这个时候模型性能由带宽和模型自身计算能力决定。这个时候只需要增加带宽，或者增加模型自身计算能力就可以提升性能(理论上)

绿色部分叫做计算瓶颈区域，不管模型计算强度怎么增加，模型的性能都不会超过红线。这个时候模型会充分压榨算力平台算力

import matplotlib.pyplot as plt
import numpy as np
# 峰值性能（Peak Performance）与内存带宽（Memory Bandwidth）
peak_performance = 100 # 以 GFLOPS 表示, 处理器可以达到的最大浮点运算性能
memory_bandwidth = 10 # 以 GB/s 表示, 内存与处理器之间每秒可以交换的最大数据量
# 设置算术密集度的范围（FLOPS/Byte）
arithmetic_intensity = np.logspace(-2, 2, num=100)
# 计算绩效上限
performance_limit = np.minimum(peak_performance, memory_bandwidth * arithmetic_intensity)
# 绘制 Roofline 模型
plt.loglog(arithmetic_intensity, performance_limit, label='Roofline')
app_arithmetic_intensity = 0.2 # FLOPS/Byte 运算量/访存量
app_peak_performance = 0.8 # 每秒进行的浮点运算次数
# 标记应用程序性能
plt.scatter(app_arithmetic_intensity, app_peak_performance, color='red', label='App Performance')
# 添加图例和标签
plt.xlabel('Arithmetic Intensity (FLOPS/Byte)')
plt.ylabel('Performance (GFLOPS)')
plt.legend()
plt.grid(True, which="both", ls="--")
plt.title('Roofline Model')
# 显示图表
plt.show()

优化手段可以分为两类 1. 提高算力 2. 提高带宽

对于 Memory-bound(红色) 的任务，优化内存带宽更加有效；而对于 Compute-bound(绿色) 的任务，则应该优化算力