ControlNet笔记

作者的代码开源在GitHub。

想要体验ControlNet看我的文章

介绍

作者在文章开头先对当前大型text-to-image model提出了疑问：这种基于提示的控制是否满足我们的需求？例如在图像处理中，考虑许多具有明确问题公式的长期任务，这些大型模型能否被应用于促进这些特定任务？我们应该建立什么样的框架来处理广泛的问题条件和用户控制？在特定任务中，大型模型能否保持从数十亿图像中获得的优势和能力？

does this prompt-based control satisfy our needs? For example in image processing, considering many long-standing tasks with clear problem formulations, can these large models be applied to facilitate these specific tasks? What kind of framework should we build to handle the wide range of problem conditions and user controls? In specific tasks, can large models preserve the advantages and capabilities obtained from billions of images?

接下来，作者提供了他们研究了大量模型后的发现 1. 需要具有鲁棒性的神经网络训练方法来避免过度拟合，并在针对特定问题训练大型模型时保持泛化能力。 2. 当图像处理任务使用数据驱动解决方案处理时，不可能总是使用大型计算集群，因此快速训练方法对于在可接受的时间和内存空间（例如在个人设备上）内将大型模型优化到特定任务很重要。这将进一步要求利用预训练的权重，以及微调策略或迁移学习。 3. 各种图像处理问题有不同的问题定义、用户控制或图像注释形式。考虑到一些特定的任务，如深度到图像、姿势到人等，这些问题本质上需要将原始输入解释为对象级或场景级别的理解，使得手工制作的程序方法不太可行。为了在许多任务中实现学习到的解决方案，端到端学习是必不可少的。

ControlNet可以用多种数据类型作为训练数据，例如Canny edges, Hough lines, user scribbles, human key points, segmentation maps, shape normals, depths, etc.

ControlNet也可以在个人计算机上进行训练，实现在有大型显存和多个gpu的集群上训练一样的效果。

模型结构

ControlNet是一种端到端的网络，他将正常的网络参数变成了两份："trainable copy" and "locked copy"。

• "locked copy" 保留了从数十亿张图像中学习到的网络能力
• "trainable copy" 在特定于任务的数据集上进行训练以学习条件控制。

"trainable copy" 和 "locked copy"用一种称为“zero convolution”的卷积层连接，其中卷积权重逐渐从零增长到以学习方式优化参数。"zero convolution"即1 * 1卷积

方法

网络架构

ControlNet 操纵神经网络块的输入条件，以进一步控制整个神经网络的整体行为。

以2D图像为例，给定一张图像(特征图)\(\boldsymbol{x}\in\mathbb{R}^{h\times w\times c}\) ,\(h,w,c\) 分别代表高度，宽度，深度。一个将x转换为y的神经网络我们可以以将他记作\(\mathcal{F(\cdot;\Theta)}\)

\[\boldsymbol{y}=\mathcal{F}(\boldsymbol{x};\Theta)\]

我们把zero convolution记作\(\mathcal{Z}(\cdot;\cdot)\) ,那么ControlNet就可以记作\[\begin{matrix}\boldsymbol{y_c}=\mathcal{F}(\boldsymbol{x};\Theta)+\mathcal{Z}(\boldsymbol{F}(\boldsymbol{x}+\mathcal{Z}(\boldsymbol{c};\Theta_{\text{z1}});\Theta_{\text{z2}})\end{matrix}\]

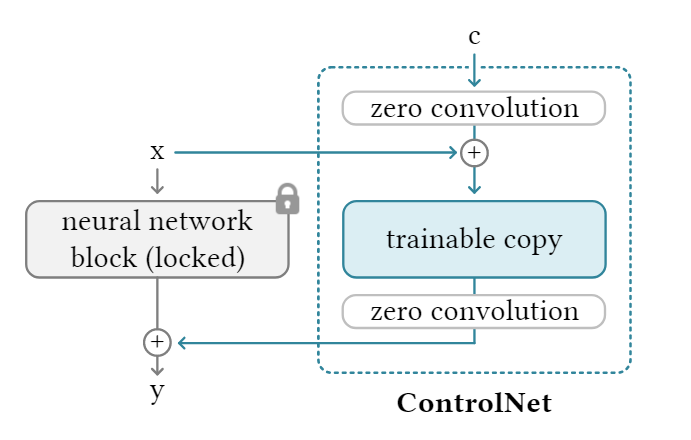
由于zero convolution的权重初始为0，那么就有\[\begin{cases}\mathcal{Z}(c;\Theta_{\text{z1}})=\mathbf{0}\\ \mathcal{F}(\boldsymbol{x}+\mathcal{Z}(\boldsymbol{c};\Theta_{\text{z1}});\Theta_{\text{c}})=\mathcal{F}(\boldsymbol{x};\Theta_{\text{c}})=\mathcal{F}(\boldsymbol{x};\Theta_{\text{c}})\\ \mathcal{Z}(\mathcal{F}(\boldsymbol{x}+\mathcal{Z}(\boldsymbol{c};\Theta_{\text{z1}});\Theta_{\text{c}});\Theta_{\text{z2}})=\mathcal{Z}(\mathcal{F}(\boldsymbol{x};\Theta_{\text{c}});\Theta_{\text{z2}})=\mathbf{0}\end{cases}\] 可以得出\(y_c=y\),即当ControlNet被应用到任何一个网络上时，不会对这个网络的效果产生任何影响。它完美保留了任何神经网络块的能力、功能和结果质量，任何进一步优化都将随着微调而变得快速

作者也推导了zero convolution的梯度。网络的前向过程可以写成\[\mathcal{Z}(\boldsymbol{I};\{\boldsymbol{W},\boldsymbol{B}\})_{p,i}=\boldsymbol{B}_{i}+\sum_{j}^{c}\boldsymbol{I}_{p,i}\boldsymbol{W}_{i,j}\] 在最开始，zero convolution 的参数\(W\)和\(B\) 都是0，只要输入\(I\)不为0，那么就有 \[\begin{cases}\dfrac{\partial\mathcal{Z}(\textbf{I};\{\textbf{W},\textbf{B}\})_{p,i}}{\partial\textbf{B}_i}=1\quad\\ \frac{\partial\mathcal{Z}(\mathbf{I};\{\mathbf{W},\mathbf{B}\})_{p,i}}{\partial\mathbf{I}_{p,i}}=\sum_{j}^{c}\mathbf{W}_{i,j}=0 \\ \frac{\partial\mathcal{Z}(\mathbf{I};\{W,\mathbf{B}\})_{p,i}}{\partial W_{i,j}}=\mathbf{I}_{p,i}\neq\mathbf{0} \end{cases}\] 我们可以看到，虽然zero convolution会导致\(I\) 上的梯度变为零，但权重和偏差的梯度不受影响。只要特征 \(I\) 非零，权重 \(W\) 将在第一个梯度下降迭代中优化为非零矩阵.考虑经典的梯度下降\[W^*=W-\beta_{\mathbb{If}}\cdot\dfrac{\partial\mathcal{L}}{\partial\mathcal{Z}(\mathbf{I};\{W,B\})}\odot\dfrac{\partial\mathcal{Z}(\mathbf{I};\{W,B\})}{\partial W}\neq\mathbf{0}\] \(W*\) 代表了第一次梯度下降之后的权重，\(\odot\) 是Hadamard product，即对应的各个元素相乘(\(c_{ij}=a_{ij}×b_{ij}\)) 。

在这一步之后，我们可以得到\[\dfrac{\partial\mathcal{Z}(\mathbf{I};\{\mathbf{W}^*,\mathbf{B}\})_{p,i}}{\partial\mathbf{I}_{p,i}}=\sum\limits_j^c\mathbf{W}_{i,j}^*\neq\mathbf{0}\] 这里包含了非零的梯度并且神经网络开始学习。这样，零卷积就变成了一种独特的连接层，它以学习的方式从零逐步增长到优化的参数。

在stable diffusion上的ControlNet

咕咕咕(以后补上)

训练

图像扩散模型是学习逐步去噪图像以生成样本。去噪可能发生在像素空间或从训练数据中编码的Latent Space中。stable diffusion使用latent image作为训练域。在这种情况下，术语"image", "pixel"和"denoising"都指的是“latent space”中的相应概念

给定图像 \(z_0\)，扩散算法逐渐向图像添加噪声并产生噪声图像 \(z_t\)，其中 t 是添加噪声的次数。当 \(t\) 足够大时，图像近似于纯噪声。给定一组条件，包括时间步 \(t\)、文本提示 \(c_t\) 以及特定于任务的条件 \(c_f\)，图像扩散算法学习网络 \(\epsilon_{\theta}\) 以预测添加到噪声图像的噪声 \(z_t\),对于\[\mathcal{L}=\mathbb{E}_{\boldsymbol{z}_0,t,\boldsymbol{c}_t,\boldsymbol{c}_i,\boldsymbol{\epsilon}\mathcal{N}(0,1)}\bigg[\|\epsilon-\epsilon_\theta(z_t,t,\boldsymbol{c}_t,\boldsymbol{c}_\mathbb{I}))\|_2^2\bigg]\] 其中\(\mathcal{L}\) 是整个扩散模型的整体学习目标。这种学习目标可以直接用于微调扩散模型。

在训练过程中，作者随机的将50%的prompt换成了空的prompt，作者认为这可以增强模型从文本内容识别语义信息的能力。这主要是因为当 stable diffusion 模型看不到提示时，decoder倾向于从输入控制图中学习更多的语义作为提示的替代品。

改进训练

作者在这一节讨论了两种极端情况，分别是计算设备及其有限时例如个人电脑，和计算设备机器充足时

Small-Scale Training

当计算设备有限时，作者发现部分打破ControlNet与stable diffusion之间的联系可以加速收敛。默认情况下是将ControlNet连接到“SD Middle Block”和“SD Decoder Block 1,2,3,4”。作者发现，只连接Middle Block而不连接Decoder Block 1,2,3,4可以将训练速度提高1.6倍(在RTX 3070TI笔记本电脑GPU上测试)。当模型在结果和条件之间表现出合理的关联时，这些断开连接的链接可以在持续训练中再次连接，以促进精确控制。

Large-Scale Training

在这里，大规模训练是指可以使用强大的计算集群（至少 8 个 Nvidia A100 80G 或等效）和大型数据集（至少 100 万个训练图像对）的情况。这通常适用于数据很容易获得的任务，例如，由canny检测到的边缘图。在这种情况下，由于过拟合的风险相对较低，可以训练 ControlNets 进行大量迭代（通常为 50k 多个步骤），然后解锁稳定扩散的所有权重并联合训练整个模型作为一个整体。这将导致更具体的问题模型(This would lead to a more problem-specific model.)。

实验

设置

作者的实验是在\(CFG-scale=9.0\) 进行的，采样器是DDPM。默认的步数是20步，在模型采取了三种 prompt

prompt

1. No prompt：也就是""
2. Default prompt:由于stable diffusion本质上是使用prompt进行训练的，因此空字符串可能是模型的意外输入，如果没有提供提示，SD 往往会生成随机纹理图。更好的设置是使用无意义的提示，"an image", "a nice image", "a professional image",etc。在作者的设置中，我们使用"a professional, detailed, high-quality image"作为default prompt。
3. Automatic prompt:为了测试fully automatic pipeline的SOTA，作者还尝试使用fully automatic pipeline（例如，BLIP）使用“default prompt”模式获得的结果生成prompts。作者会使用生成的提示再次扩散。
4. User prompt：用户自定义的输入